A Note About the Exponential Distribution (Failure Rate or MTBF)

When deciding whether an item should be replaced preventively, there are two requirements that must be met: the item’s reliability must get worse with time (i.e., it has an increasing failure rate) and the cost of preventive maintenance must be less than the cost of the corrective maintenance. If both of these requirements are not met, then preventive maintenance will not be effective, either on a reliability basis or on a cost basis.

If you want to use mean time before/between failure (MTBF) or failure rate to describe the probability of failure, then you will be defining a constant failure rate (i.e., a rate that does not vary with time). In other words, you are assuming an exponential distribution. On the Settings page of the Application Setup, RCM++ provides two options for defining the exponential parameter: Lambda (which is also called failure rate) or Mean Time (which is also called MTBF).

Therefore, it is important to note that if the equipment’s failure behavior follows an exponential distribution, then preventive maintenance will not improve the overall reliability of the equipment. The following simple example illustrates this point.

Suppose that two components follow an exponential distribution with MTBF = 100 hours (or failure rate = 0.01). Component 1 is preventively replaced every 50 hours, while component 2 is never maintained. If we compare the reliabilities of the two components from 0 to 60 hours:

• Component 1, with PM: With PM, the reliability from 0 to 60 hours is based on the reliability of the original item operating for 50 hours, R(t=50)=60.65%, multiplied by the reliability of the new item operating for 10 hours, R(t=10)=90.48%. The overall result is 54.88%.
• Component 2, without PM: Without PM, the reliability from 0 to 60 hours is based on the reliability of the original item operating to 60 hours, R(60)=54.88%.

Likewise, if we compare the reliabilities of the two components from 50 to 60 hours:

• Component 1, with PM: With PM, the reliability from 50 to 60 hours is based on the reliability of the new item operating for 10 hours, R(t=10)=90.48%.
• Component 2, without PM: Without PM, the reliability from 50 to 60 hours is based on the conditional reliability of the original item operating to 60 hours, having already survived to 50 hours, or RC(T=60|50)=R(60)/R(50)=90.48%.

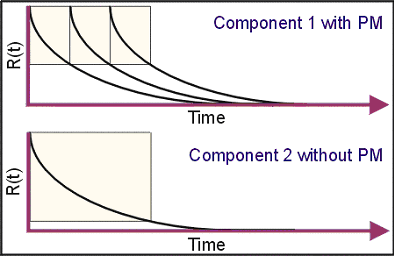
As this example demonstrates, both maintenance strategies result in the same reliability. In other words, the preventive maintenance does not improve the equipment’s reliability. If you choose to perform preventive maintenance on equipment that does not exhibit an increasing failure rate (i.e., wearout), you may be wasting resources on maintenance actions that provide no benefit. In addition, the unnecessary maintenance may actually reduce the equipment’s reliability by reintroducing infant mortality and/or introducing new failures due to maintenance errors.