Parametric RDA Example
The data set used in this example is available in the example database installed with the Weibull++ software (called "Weibull20_Examples.rsgz20"). To access this database file, choose File > Help, click Open Examples Folder, then browse for the file in the Weibull sub-folder.
The name of the project is "Parametric RDA - Airplane AC Repair."
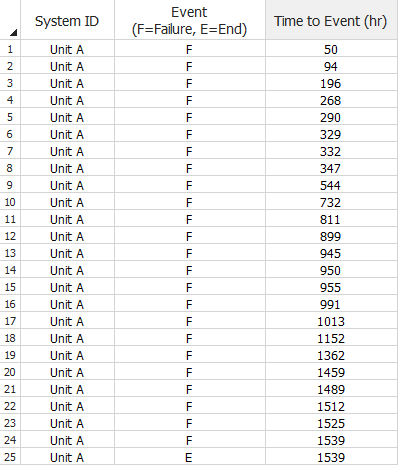
An analyst recorded the successive failures of the air-condition unit of an aircraft. The objective is to obtain the expected number of failures that may occur by 1,800 hours. The following data sheet shows the failure logs of the unit between 0 to 1,539 hours of observation. The observation period ended at the time of the last failure.
Analyze the Data Set
The first step is to determine which virtual age model provides the best statistical fit for the given data. On the Main page of the control panel, select 3 for the parameters settings and then calculate the results for each of the virtual age models. Use the default settings for the simulation.
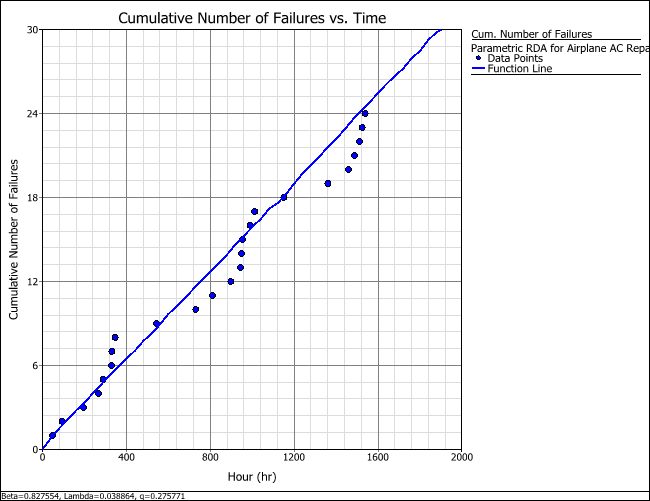
The LK value for the Type I model is -123.6347 while the LK value for the Type II model is -123.5964. Therefore, for this data set, the Type II model may provide the best fit (i.e., have a slightly larger LK value). The parameters of the Type II GRP model are estimated to be beta = 0.8276, lambda = 0.0389 and q = 0.2758.
Click the Plot icon to visualize how the number of failures increases over time, as shown next.
To estimate the number of failures expected to occur by 1,800 hours, click the QCP icon on the control panel. In the QCP, choose to calculate the Cumulative Number of Failures with two-sided confidence bounds. Select Hour for the time units and then make the following inputs:
Mission Start Time: 0
Mission Additional Time: 1800
Confidence Level: 0.9
Click Calculate. The results show that the cumulative number of failures in 1,800 hours is 28.4740 or about 28 failures, and the number may be as high as about 39 failures.
