Multiple Linear Regression Folio: Plots
The following plots may be available on the Analysis Plot tab of the multiple linear regression folio. Note that the contour plot and residual vs. factor plot are available only when there are at least two factors included in the analysis. For general information on working with plots, see Plot Utilities.
Effect Plots
Effect plots allow you to visually evaluate the effects of factors and factorial interactions on the selected response.
The Pareto Chart - Regression plot shows the standardized effects of the selected terms (i.e., factor or combination of factors). The vertical blue line is the threshold value. If a bar is beyond the blue line, it will be red, indicating that the effect is significant.
The Pareto Chart - ANOVA* plot shows the inverse p value (1 - p) of each selected term. The vertical blue line is the threshold value. If a bar is beyond the blue line, it will be red, indicating that the term is significant.
The Scatter Plot shows the observed values of the currently selected response plotted against the levels of the selected factor. A 3-dimensional version of this plot is available in the 3D plot folio.
The Contour Plot shows how varying two selected factors affects the predicted response values, which are represented as colors. See Contour Plots. A 3-dimensional version of this plot ("Surface Plot") is available in the 3D plot folio. For mixture designs, this plot applies only to process factors (i.e., process variables).
Residual Plots
Residuals are the differences between the observed response values and the response values predicted by the model at each combination of factor values. Residual plots help to determine the validity of the model for the currently selected response. When applicable, a residual plot allows the user to select the type of residual to be used:
Regular Residual is the difference between the observed Y and the predicted Y.
Standardized Residual is the regular residual divided by the constant standard deviation.
Studentized Residual is the regular residual divided by an estimate of its standard deviation.
External Studentized Residual is the regular residual divided by an estimate of its standard deviation, where the observation in question is omitted from the estimation.
The plots are described next.
The Residual Probability* plot is the normal probability plot of the residuals. If all points fall on the line, the model fits the data well (i.e., the residuals follow a normal distribution). Some scatter is to be expected, but noticeable patterns may indicate that a transformation should be used for further analysis. Two additional measures of how well the normal distribution fits the data are provided by default in the lower title of this plot. Smaller values for the Anderson-Darling test indicate a better fit. Smaller p values indicate a worse fit.
The Residual vs. Fitted* plot shows the residuals plotted against the fitted, or predicted, values of the selected response. If the points are randomly distributed around the "0" line in the plot, the model fits the data well. If a pattern or trend is apparent, it can mean either that the model does not provide a good fit or that Y is not normally distributed, in which case a transformation should be used for further analysis. Points outside the critical value lines, which are calculated based on the specified alpha (risk) value, may be outliers and should be examined to determine the cause of their variation.
The Residual vs. Order* plot shows the residuals plotted against the order of runs used in the design. If the points are randomly distributed in the plot, it means that the test sequence of the experiment has no effect. If a pattern or trend is apparent, this indicates that a time-related variable may be affecting the experiment and should be addressed by randomization and/or blocking. Points outside the critical value lines, which are calculated based on the specified alpha (risk) value, may be outliers and should be examined to determine the cause of their variation.
The Residual vs. Factor* plot shows the residuals plotted against values of the factor selected in the Residual Factor area. It is used to determine whether the residuals are equally distributed around the "0" value line and whether the spread and pattern of the points are the same at different levels. If the size of the residuals changes as a function of the factor’s settings (i.e., the plot displays a noticeable curvature), the model does not appropriately account for the contribution of the selected factor. Points outside the critical value lines, which are calculated based on the specified alpha (risk) value, may be outliers and should be examined to determine the cause of their variation.
The Residual Histogram* is used to demonstrate whether the residual is normally distributed by dividing the residuals into equally spaced groups and plotting the frequency of the groups. The Residual Histogram Settings area allows you to:
Select Custom Bins to specify the number of groups, or bins, into which the residuals will be divided. Otherwise, the software will automatically select a default number of bins based on the number of observations.
Select Superimpose pdf to display the probability density function line on top of the bins.
The Residual Autocorrelation* plot shows a measure of the correlation between the residual values for the series of runs (sorted by run order) and one or more lagged versions of the series of runs. The default number of lags is the number of observations, n, divided by 4. If you select Custom Lags in the Auto-Correlation Options area, you can specify up to n -1 lags. The correlation is calculated as follows:
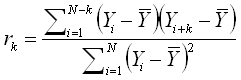
where:
k is the lag.
 is the mean value of the original series
of runs.
is the mean value of the original series
of runs.
For example, lag 1 shows the autocorrelation of the residuals when run 1 is compared with run 2, run 2 is compared with run 3 and so on. Lag 3 shows the autocorrelation of the residuals when run 1 is compared with run 4, run 2 is compared with run 5 and so on. Any lag that is displayed in red is considered to be significant; in other words, there is a correlation within the data set at that lag. This could be caused by a factor that is not included in the model or design, and may warrant further investigation.
The Fitted vs. Actual plot shows the fitted, or predicted, values of the currently selected response plotted against the observed values of the response. If the model fits the data well, the points will cluster around the line.
Diagnostic Plots
The Leverage vs. Order plot shows leverage plotted against the order of runs used in the design. Leverage is a measure (between 0 and 1) of how much a given run influences the predicted values of the model, where 1 indicates that the actual response value of the run is exactly equal to the predicted value (i.e. the predicted value is completely dependent upon the observed value). Points that differ greatly from the rest of the runs are considered outliers and may distort the analysis.
The Cook’s Distance* plot can show Cook’s distance (i.e., a measure of how much the output is predicted to change if each run is deleted from the analysis) plotted against either the run order or the standard order for the currently selected response. Points that differ greatly from the rest of the runs are considered outliers and may distort the analysis.
The Box-Cox Transformation* plot can help determine, for the currently selected response and model, what transformation, if any, should be applied. The plot shows the sum of squares of the residuals plotted against lambda. The value of lambda at the minimum point of this curve is considered the "best value" of lambda, and indicates the appropriate transformation, which is also noted by default in the lower title of the plot.
* These plots are available only when there is error in the design, indicated by a positive value for sum of squares for Residual in the ANOVA table of the analysis results.