Extreme Vertex Designs: Example
The data set used in this example is available in the example database installed with the software (called "Weibull20_DOE_Examples.rsgz20"). To access this database file, choose File > Help, click Open Examples Folder, then browse for the file in the Weibull sub-folder.
The name of the example project is "Mixture Design - Extreme Vertex Design."
Four components, A, B, C and D, are used to make a polymer material. Their proportions are restricted by lower and upper bounds, and two linear constraints:
Bounds:
-
0.20 ≤ A ≤ 0.65
-
0.10 ≤ B ≤ 0.55
-
0.10 ≤ C ≤ 0.20
-
0.15 ≤ D ≤ 0.35
Linear constraints:
-
0.25 ≤ A + C ≤ 0.70
-
0.25 ≤ C + D ≤ 0.45
The objective of the experiment is to find the best settings of each component in order to maximize the strength of the material. An experiment within the feasible region defined by the above constraints should be conducted. The experimenters want some experiment runs to be placed at the boundary of the feasible region and some to be inside the region.
Designing the Experiment
The experimenters create an extreme vertex design folio, perform the experiment according to the design, and then enter the response values into the folio for analysis. The design matrix and the response data are given in the "Extreme Vertex Design" folio. The following steps describe how to create this folio on your own.
-
Choose Home > Insert > Mixture Design to add a mixture design folio to the current project.
![]()
-
In the folio's navigation panel, under the Design for Mixture Factors heading, click Design Type and then select Extreme Vertex in the input panel.
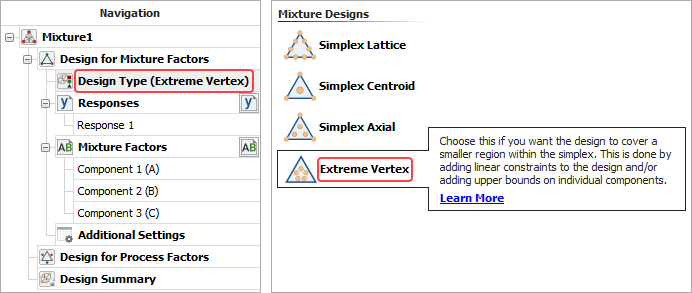
-
Specify the number of mixture factors by clicking the Mixture Factors heading in the navigation panel and choosing 4 from the Number of Factors drop-down list.
-
Define each factor by clicking it in the navigation panel and editing its properties in the input panel. The bounds for each factor are given above. The first factor is defined as shown next.
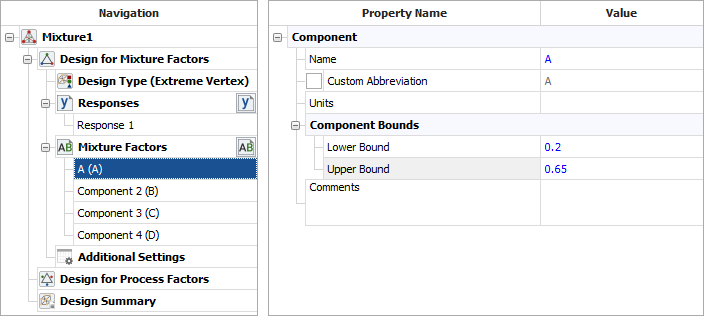
-
Rename the folio by clicking the Mixture1 heading in the navigation panel and entering Extreme Vertex Design for the Name in the input panel.
-
Click the Additional Settings heading to choose the number of center points and axial points per vertex, and to specify the linear constraints.
-
-
Set the number of Center Points to 1.
-
Set the Axial per Vertex field to 1.
-
Click the [+] icon under Linear Constraints and enter the linear constraints as shown next.
-
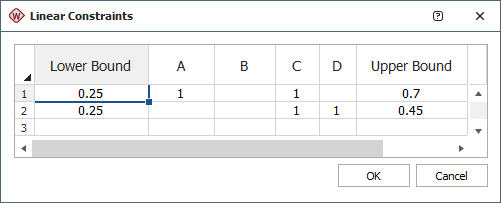
After you click OK, the constraints are displayed in the folio as shown next.
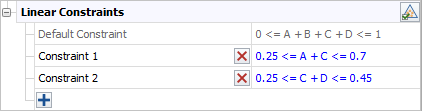
-
-
To determine whether you have entered any incompatible or unnecessary linear constraints, click the Validate Constraints icon next to the Linear Constraints heading.
-
![]()
No constraints are marked as problematic, so you can proceed.
-
Finally, click the Build icon on the control panel to create a Data tab that allows you to view the test plan and enter response data.
![]()
Analysis and Results
The data set for this example is given in the "Extreme Vertex Design" folio of the example project. After you enter the data from the folio, you can perform the analysis by doing the following:
Note: To minimize the effect of unknown nuisance factors, the run order is randomly generated when you create the design. Therefore, if you followed these steps to create your own folio, the order of runs on the Data tab may be different from that of the folio in the example file. This can lead to different results. To ensure that you get the very same results described next, show the Standard Order column in your folio, then click a cell in that column and choose Sheet > Sheet Actions > Sort > Sort Ascending. This will make the order of runs in your folio the same as that of the example file. Then copy the response data from the example file and paste it into the Data tab of your folio.
-
Make sure all terms up to 2-way interactions will be considered. To do this, click the Select Terms icon on the control panel.
![]()
In the window that appears, select the Linear and Quadratic check boxes. Then click OK.
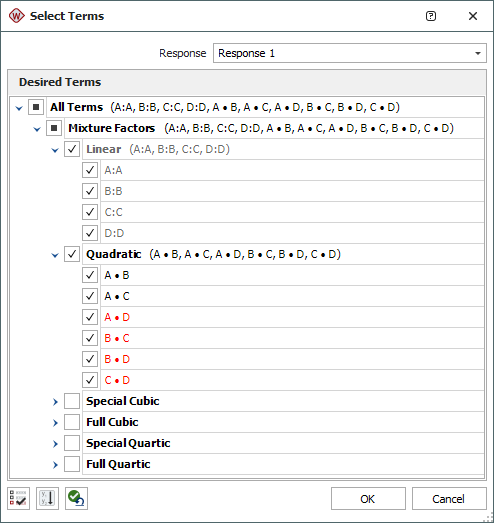
-
On the Analysis Settings page of the Control Panel, select to use Individual Terms in the analysis.
-
Click the Calculate icon.
![]()
-
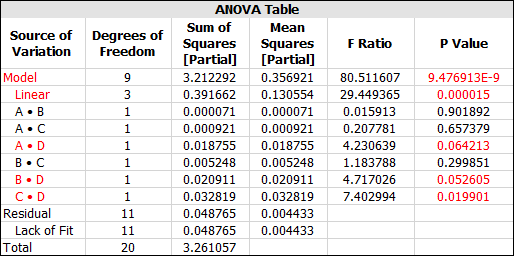
In the Analysis Summary area on the control panel, click the View Analysis Summary icon to view detailed results from the analysis. Note that the results from this step are not visible in the example folio, which shows the reduced model results that are obtained later in this example.
In the ANOVA table, you can see that effects AD, BD and CD are significant. The p value for effect BC is also relatively close to the risk level of 0.1. Therefore, you decide to include it in the final model.
Optimization
The reduced model includes only the terms that were found to be significant. The following steps describe how to obtain this model on your own.
-
Click the Select Terms icon on the control panel.
-
In the Select Terms window that appears, click the Select Significant Effects icon to select only the significant effects to calculate the new model, and also select the check box for effect BC, as shown next, then click OK.
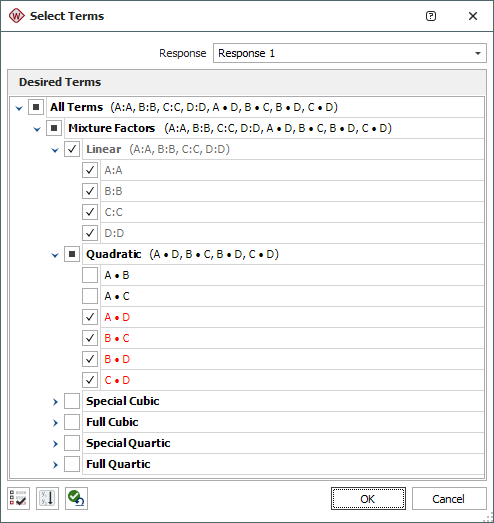
-
Click the Calculate icon in the control panel.
-
In the Analysis Summary area on the control panel, click the View Analysis Summary icon to view detailed results from the analysis.
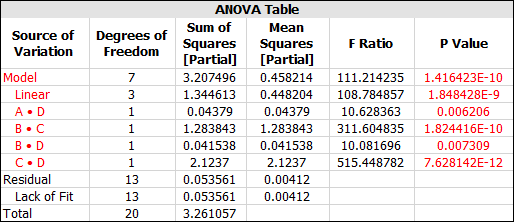
-
Click the Design - Optimization icon on the control panel.
![]()
-
In the Response Settings window that appears, use the settings shown next and click OK. These settings indicate that you want to maximize Response 1, with values above 3.5 being considered 100% desirable and values below 3.0 being undesirable.
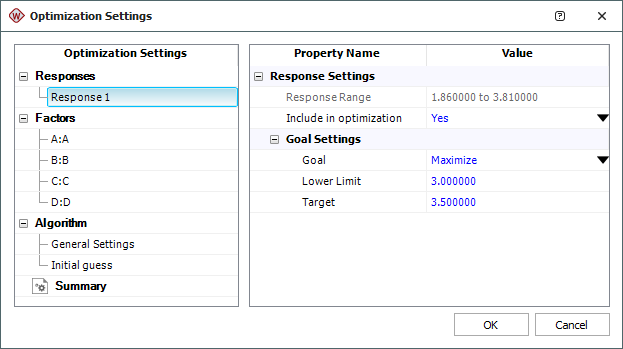
-
An Optimization folio will appear with a plot showing the single solution that is found.
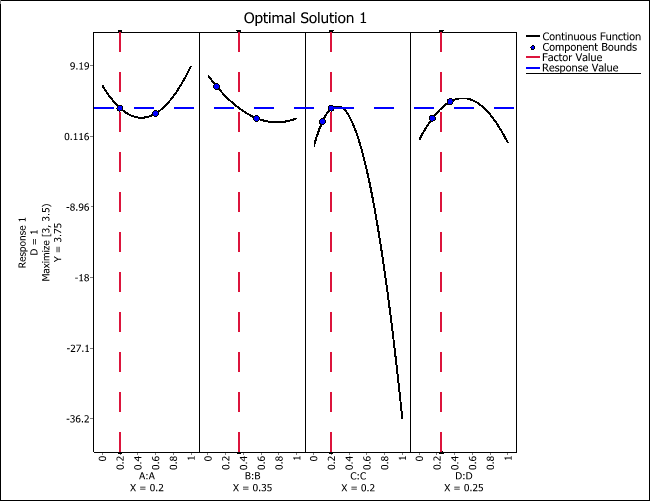
-
You can choose Optimization > Solutions > View Solutions or click the icon on the control panel to see the solution in numerical format.
![]()
The optimum settings are shown next.
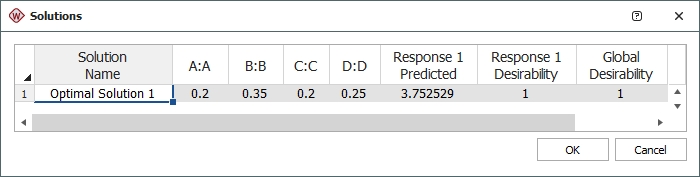
Conclusions
The optimal solution is found to be A = 0.2, B = 0.35, C = 0.2 and D = 0.25. Under this setting, the expected strength of the material is 3.75. Keep in mind that it is necessary to conduct an experiment using this setting to confirm this conclusion.