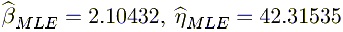ReliaSoft's Ranking Method
When analyzing interval data, it is commonplace to assume that the actual failure time occurred at the midpoint of the interval. To be more conservative, you can use the starting point of the interval or you can use the end point of the interval to be most optimistic. Weibull++ allows you to employ ReliaSoft's ranking method (RRM) when analyzing interval data. Using an iterative process, this ranking method is an improvement over the standard ranking method (SRM). This article presents an example using the two-parameter Weibull distribution to illustrate how this method is employed. This method can also be easily generalized for additional models.
Step-by-Step Example
Consider the test data shown in Table 1.
| Number of Items | Type | Last Inspection | Time |
| 1 | Exact Failure | 10 | |
| 1 | Right Censored | 20 | |
| 2 | Left Censored | 0 | 30 |
| 2 | Exact Failure | 40 | |
| 1 | Exact Failure | 50 | |
| 1 | Right Censored | 60 | |
| 1 | Left Censored | 0 | 70 |
| 2 | Interval Failure | 20 | 80 |
| 1 | Interval Failure | 10 | 85 |
| 1 | Left Censored | 0 | 100 |
Table 1: Test data
As a preliminary step, we need to provide a crude estimate of the Weibull parameters for this data. To begin, we will extract the exact times-to-failure (10, 40 and 50) and append them to the midpoints of the interval failures: 50 (for the interval of 20 to 80) and 47.5 (for the interval of 10 to 85). Now, the extracted list consists of the data in Table 2.
| Number of Items | Type | Last Inspection | Time |
| 1 | Exact Failure | 10 | |
| 2 | Exact Failure | 40 | |
| 1 | Exact Failure | 47.5 | |
| 3 | Exact Failure | 50 |
Table 2: Union of exact times-to-failure with the midpoint of the interval failures
Using the traditional rank regression, we obtain the first initial estimates:

Step 1
For all intervals, we obtain a weighted "midpoint" using:
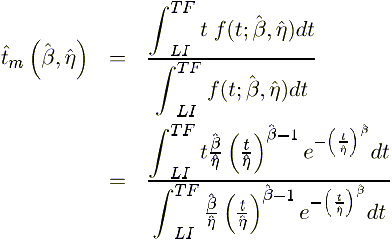
This transforms the data into the format displayed in Table 3.
| Number of Items | Type | Last Inspection | Time | Weighted Midpoint |
| 1 | Exact Failure | 10 | ||
| 2 | Exact Failure | 40 | ||
| 1 | Exact Failure | 50 | ||
| 2 | Interval Failure | 20 | 80 | 42.837 |
| 1 | Interval Failure | 10 | 85 | 39.169 |
Table 3: Union of exact times-to-failure with the midpoint based on parameters β and η
Step 2
Now arrange the data, as shown in Table 4.
| Number of Items | Time |
| 1 | 10 |
| 1 | 39.169 |
| 2 | 40 |
| 2 | 42.837 |
| 1 | 50 |
Table 4: Union of exact times-to-failure in ascending order
Step 3
Now consider the left and right censored data shown in Table 5.

Table 5: Computation of
increments for computing a revised mean order number
In general, for left censored data:
The increment term for n left censored
items at time = t0, with a time-to-failure of ti,
when t0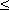 ti-1 is zero.
ti-1 is zero.
When t0 > ti-1 the contribution is:

Or:
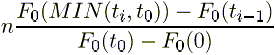
Where ti-1 is the time-to-failure previous to the ti time-to-failure and n is the number of units associated with that time-to-failure (or units in the group).
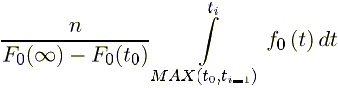
Or:
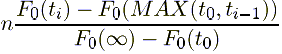
Step 4
Sum up the increments (horizontally in rows) as shown in Table 6.

Table 6: Increments
solved numerically
Step 5
Compute new mean order numbers (MON), as shown in Table 7, utilizing the increments obtained in Table 6, by adding the "number of items" plus the "previous MON" plus the current "increment."
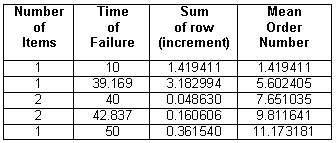
Table 7 - Mean Order
Numbers (MON)
Step 6
Compute the median ranks based on these new MONs, as shown in Table 8.
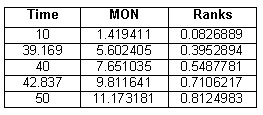
Table 8 - Mean Order
Numbers with ranks for a sample size of 13 units
Step 7
Compute new Beta and Eta using standard rank regression and based upon the data as shown in Table 9.

Table 9 - New times and
median ranks for regression
Step 8
Return and repeat the process from Step 1 until an acceptable convergence is reached on the parameters (i.e., until the parameter values stabilize).
Results
The results of the first five iterations are shown in Table 10.

Table 10 - The
parameters after the first five iterations
Using Weibull++ with rank regression on X yields:
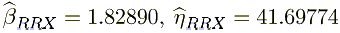
The direct MLE solution yields: