Determining the Reliability of a System with Standby Redundancy
In the last issue of the HotWire, we discussed the case of a system with load sharing components. Load sharing is a form of redundancy with dependent components, i.e., the failure of one component affects the likelihood of failure for the other component(s). In this issue, we will discuss another form of redundancy, namely standby. This article describes the three types of standby configurations (hot, warm and cold) and presents an example analysis for a system with one active and one standby component.
Under standby redundancy, the redundant components do not share any of the load, and they start operating only when active components fail. In standby redundancy, the components are divided into two types, Active and Standby. The standby components have two failure distributions. One for when they are in standby (quiescent distribution) and one for when they operate (active distribution).
When the failure rate of the standby component is the same in quiescent mode as it is in active mode, then components are in a "hot standby" configuration. This is the same type of redundancy as the simple parallel. When the failure rate of the standby component is less in quiescent mode than in active mode, then you have a "warm standby" configuration. Lastly, when the failure rate of the standby component is zero in quiescent mode (i.e. the component cannot fail when in standby), then you have a "cold standby" configuration.
Example
Consider two components in standby configuration. Component 1 is the active component with a Weibull failure distribution (beta=1.5, eta=1000). Component 2 is the standby component. When Component 2 is operating, it has a Weibull failure distribution with beta=1.5 and eta=1000. Note: Even though Components 1 and 2 have the same distribution and parameters, it is possible that the two can be different. For the quiescent distribution, consider three different scenarios:
- Same distribution as when in operation (hot standby).
- beta=1.5, eta=2000 (warm standby).
- Cannot fail in quiescent mode (cold standby).
What is the system reliability at 1000 hours? Note: For this example, we will only consider the non-repairable case, i.e., when a component fails, it is not repaired/replaced.
The reliability of the system at some time, t, can be calculated using the following equation:
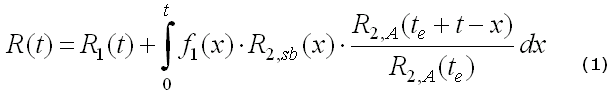
where,
- R1 is the reliability of the active component
- f1 is the pdf of the active component
- R2,sb is the reliability of the standby component when in standby mode (quiescent reliability)
- R2,A is the reliability of the standby component when in active mode
- te is the equivalent operating time for the standby unit if it had been operating at an active mode, such that:
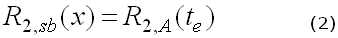
Solving Eqn. (2) with respect to te, you can obtain an expression for the equivalent time, which can then be substituted into Eqn. (1).
BlockSim includes the ability to calculate standby redundancy. The following figure illustrates the reliability block diagram (RBD) for the system as entered in BlockSim 6.
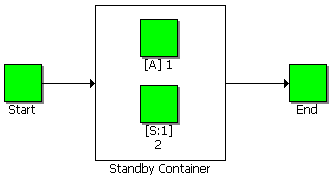
The Start and End blocks have no failure information (i.e., reliability of 100%) and therefore do not affect the reliability of the system. The active and standby blocks are within a Standby Container, which is used within BlockSim 6 RBDs to specify standby redundancy. Note: An article in Volume 3, Issue 2 of the Reliability Edge newsletter provides more detailed information on the use of Container blocks within BlockSim 6.
Since the standby component has two distributions (active and quiescent), the Block Properties window of the standby block has two pages for specifying each one.
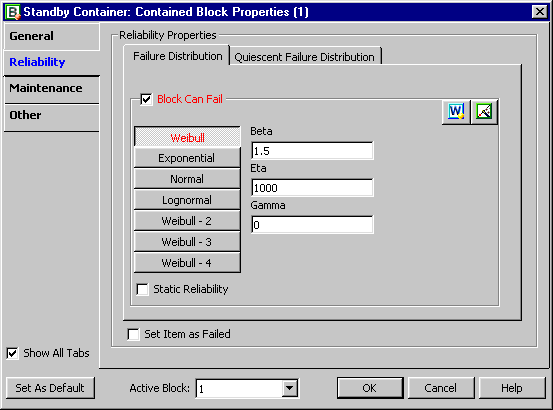
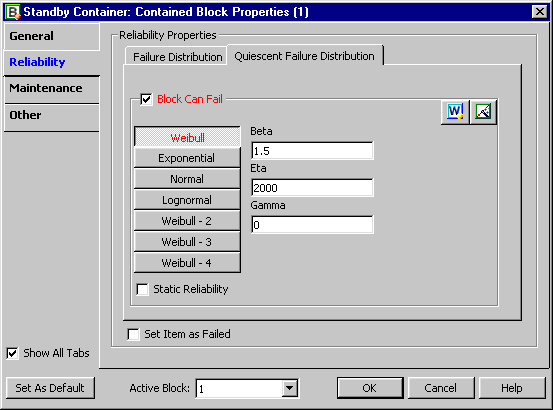
Note that even though the beta for the quiescent distribution is the same as in the active distribution, it is possible that the two can be different. In other words, there may be different failure modes present during the quiescent mode than during the active mode. For the same reason, it is also possible that two different distribution types may be used to describe the active and quiescent modes (e.g., lognormal when quiescent and Weibull when active).
The results for this example are given in the following table:
| Standby Type | System Reliability at 1000hr |
| Hot | 0.6004 |
| Warm | 0.7057 |
| Cold | 0.8212 |
In many cases when considering standby systems, there is also a switching device that switches from the failed active component to the standby component. The reliability of the switch can also be incorporated into Eqn. (1). The incorporation of the switch reliability in the standby configuration is discussed here.