Specify Points

The Specify Points feature enables you to experiment with possible alternative scenarios by allowing you to adjust the way that the line is fitted to the points for a rank regression analysis. The ranks will be calculated based on all of the data points, but the regression line (which determines the parameter estimates) will be fitted only to the points you have specified. Any plots or QCP results will be based on the adjusted line, and therefore may be appropriate only within the context of your specific "what if" analysis.

To use the Specify Points feature, first identify the data points that you wish to include in the regression line/parameter estimation. In the Weibull++ life data folio data sheet, assign the selected data points to a specific subset ID, as shown in the following example.

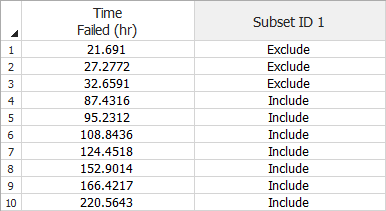
Note: The subset ID can be any text up to 30 characters, including spaces. For example, "A _ _ X" is not the same as "A _ X" where " _ " is used to designate a space.

Choose Life Data > Options > Specify Points or click the icon on the Main page of the control panel.

You will be presented with a list of all the subset IDs in your data sheet as shown next. If you have more than one subset ID column in your data sheet, a drop-down list will be available to allow you to choose which column to use in the analysis.

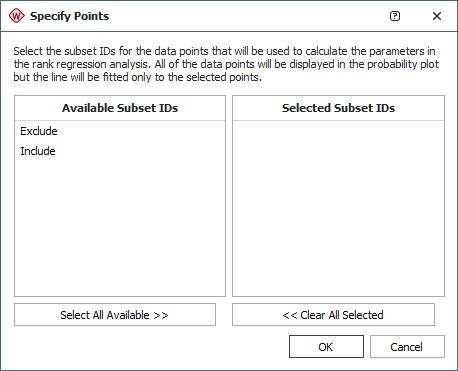
Double-click the subset ID of the data points you wish to include in the analysis (in this case, it is subset ID "Include"). You can also drag the subset ID to the Selected Subset ID column. Click OK.

Next, choose an appropriate distribution for the data set and calculate the parameters. The control panel will display the parameters of the regression model and also display a status to indicate that the standard analysis method has been altered and the parameters were calculated based on a regression line fitted only through the specified data points.

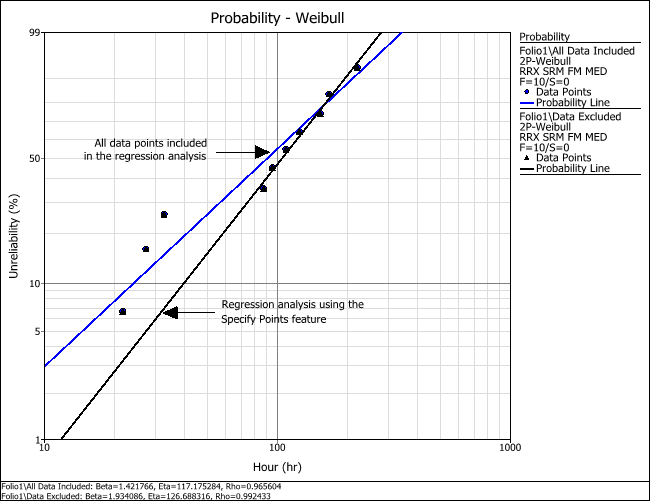
The overlay plot shown next illustrates the changes to the estimates of the parameters between the cases where the three data points are either included or excluded from the regression analysis.