About Reliability Importance
Reliability importance is a measure of how much effect each component has on the overall reliability of the system. One simple way to demonstrate this concept is to look at a series system. In general, the least reliable component in a series system has the greatest effect on the reliability of the system.
Consider three components arranged reliability-wise in series, where R1 = 70%, R2 = 80% and R3 = 85% (for a given time). In the table shown next, we can examine the effect of each component's reliability on the overall system reliability.
|
Component 1 |
Component 2 |
Component 3 |
System |
|
0.7 |
0.8 |
0.85 |
0.476 |
|
0.8 |
0.8 |
0.85 |
0.544 |
|
0.7 |
0.9 |
0.85 |
0.536 |
|
0.7 |
0.8 |
0.95 |
0.532 |
The first row of the table shows the given reliabilities for each component and the corresponding system reliability. In each of the following rows, the reliability of one component has been increased by 10% (absolute) while keeping the reliabilities of the other components at the given values. This allows us to observe the effect of each component's reliability on the overall system reliability. It is clear that the highest value for the system's reliability was achieved when the reliability of Component 1, which is the least reliable component, was increased by a value of 10%. In other words, Component 1 has a higher reliability importance.
In simple systems such as this series system configuration, it is easy to identify the weak components. However, in more complex systems this becomes quite a difficult task. The value of the reliability importance depends both on the reliability of a component and its position in the system. BlockSim calculates this value automatically.
Mathematically, reliability importance is the partial derivative of the system reliability equation with respect to a component's reliability. The reliability importance, IR, of component i in a system of n components is given by:
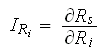
where:
- Rs is the system reliability.
- Ri is the component reliability. [Leemis, L.M., Reliability - Probabilistic Models and Statistical Methods, Prentice Hall, Inc., Englewood Cliffs, New Jersey, 1995.]
For more information about reliability importance and the various ways it is used within BlockSim, please read "Reliability Importance Measures of Components in a Complex System" at: http://www.weibull.com/hotwire/issue66/relbasics66.htm.