Test-Find-Test Data Reference Example

This example validates the results for test-find-test data in Weibull++ Reliability Growth data folios.

Reference Case

International Standard IEC 61164 (Reliability Growth in Product Design and Test – Statistical Test and Estimation Methods), Example 4, pg. 32.

For this example, the following will be calculated:

• Parameters of the Crow Extended model
• Unseen BD mode failure intensity
• Cramér-von Mises (CVM) goodness of fit for BD modes
• Demonstrated MTBF (DMTBF)
• Projected PMTBF (PMTBF)

Data

The following table shows the data.

Termination Time = 4000 hours

Failure Time	Classification Mode
150	BD1
253	BD2
475	BD3
540	BD4
564	BD5
636	A
722	BD5
871	A
996	BD6
1003	BD7
1025	A
1120	BD8
1209	BD2
1255	BD9
1334	BD10
1647	BD9
1774	BD10
1927	BD11
2130	A
2214	A
2293	A
2448	A
2490	BD12
2508	A
2601	BD1
2635	BD8
2731	A
2747	BD6
2850	BD13
3040	BD9
3154	BD4
3171	A
3206	A
3245	DB12
3249	BD10
3420	BD5
3502	BD3
3646	BD10
3649	A
3663	BD2
3730	BD8
3794	BD14
3890	BD15
3949	A
3952	BD16

BD Mode	EF
1	0.7
2	0.7
3	0.8
4	0.8
5	0.9
6	0.9
7	0.5
8	0.8
9	0.9
10	0.7
11	0.7
12	0.6
13	0.6
14	0.7
15	0.7
16	0.5

Result

The book has the following results:

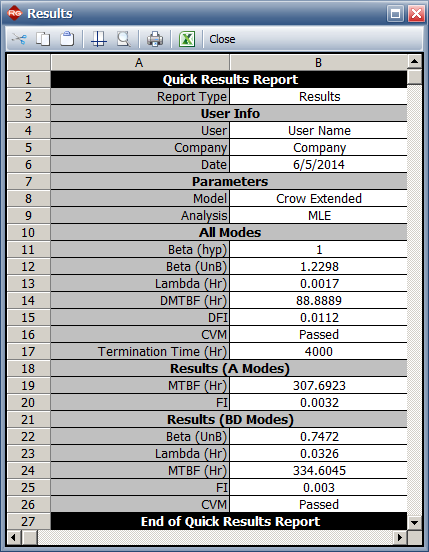
• BetaBD (UnB) = 0.7472, LambdaBD = 0.0326

• Unseen BD Mode Failure Intensity = 0.0030/hr

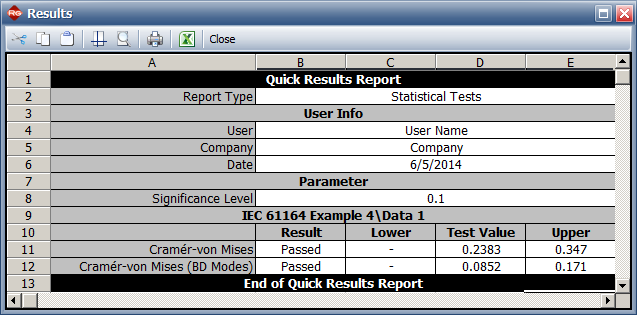
• Goodness of fit for BD modes: CVM = 0.085, critical value = 0.171 with significance level = 0.1. Since CVM < critical value can fail to reject hypothesis that the model fits the data.

• DMTBF = 88.9 hours

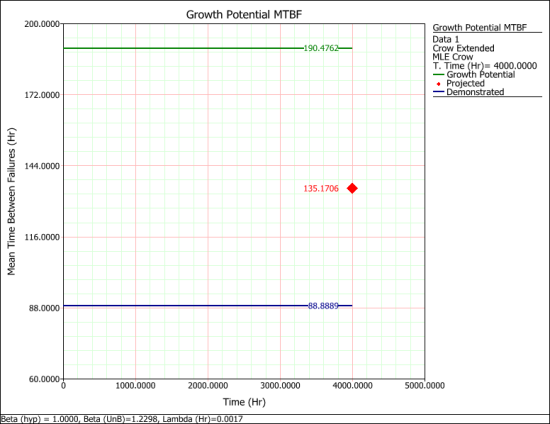
• PMTBF = 135.1 hours

Results in Weibull++

In Weibull++, the Crow Extended model with the maximum likelihood estimation (MLE) method was used to calculate the results.

For a test-find-test, the assumption is . Therefore:

• The model parameters are:

• The growth potential MTBF plot: