Repairable Systems Analysis Reference Example

This example validates the results for a repairable systems analysis in Weibull++ Reliability Growth data folios.

Reference Case

Crow, L.H., Reliability Analysis for Complex Repairable Systems, Reliability and Biometry: Statistical Analysis of Lifelength, pg. 385, 1974.

For this example, the Power Law model parameters will be calculated.

Data

The following table shows the data.

Simulated Data for 3 Systems with End Time = 200 hours

System 1	System 2	System 3
4.3	0.1	8.4
4.4	5.6	32.4
10.2	18.6	44.7
23.5	19.5	48.4
23.8	24.2	50.6
26.4	26.7	73.6
74	45.1	98.7
77.1	45.8	112.2
92.1	72.7	129.8
197.2	75.7	136
	98.6	195.8
	120.1
	161.8
	180.6
	190.8

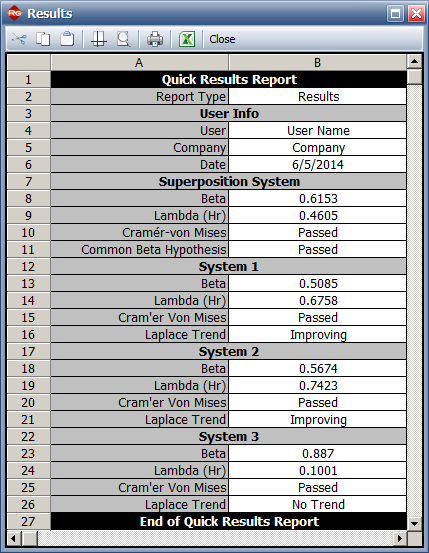
Result

The book has the following results:

Beta = 0.615, Lambda = 0.461

Results in Weibull++

Since and then the maximum likelihood estimates of and are given by:

The model parameters are: