Series Systems RBD
This example validates the results for series systems in BlockSim's analytical and simulation diagrams.
Reference Case
The data set is from example 4.2 on page 69 in the book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
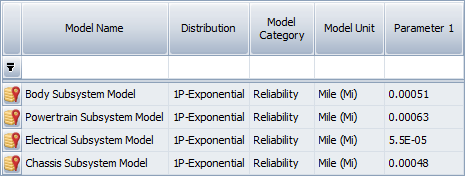
The lifetimes of the body, powertrain, electrical and chassis subsystems of a car are assumed to be exponentially distributed with the given lambdas in the table below. The reliability of the vehicle at 36,000 miles and the mean mileage to failure are calculated.
| Components of the vehicle | Number of failures, |
|---|---|
| Body | 5.1 x 10-4 |
| Powertrain | 6.3 x 10-4 |
| Electrical | 5.5 x 10-5 |
| Chassis | 4.8 x 10-4 |
Result
Substituting the values of ,
,
, and
into the equation (Equation 4.4 in the reference book) below, the lifetime of the vehicle is estimated to be 16.75 × 10-4 failures per 1000 miles.
Then, the reliability at 36,000 miles is calculated as R(36,000) = exp(-16.75 × 10-4 × 36) = 0.9415. The mean mileage to failure (MTTF) is obtained as MTTF = 1 / λ = 1 / 16.75 × 10-4 = 597,000 miles.
Results in BlockSim
In BlockSim, the vehicle RBD is configured as shown below:
Each component is modeled using a 1-parameter exponential distribution with the given lambda values. (If the exponential models show the mean times, choose
Application Setup > Calculations and then clear the Use mean time for the exponential distribution check box.):
Analytical Proof
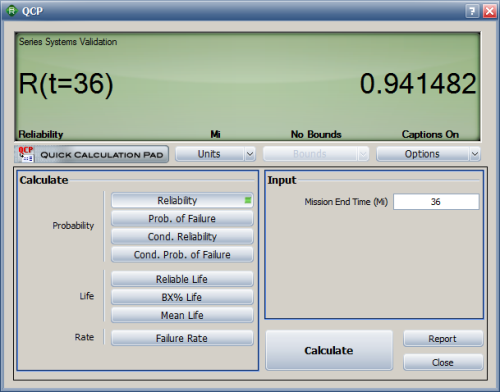
In the QCP, the reliability at 36,000 miles is estimated to be 94.1482%
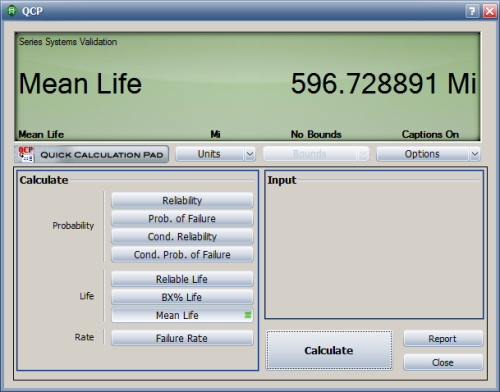
And the mean life (MTTF), which is the mileage to failure, is obtained as 596.728891 miles.
Simulation Proof
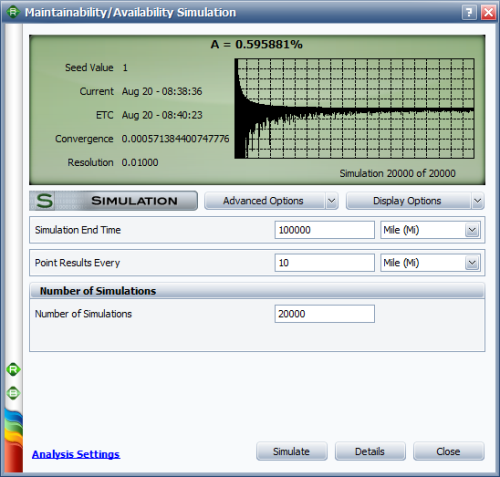
We can also estimate the results by using the simulation tool in BlockSim. The simulation settings are shown below.
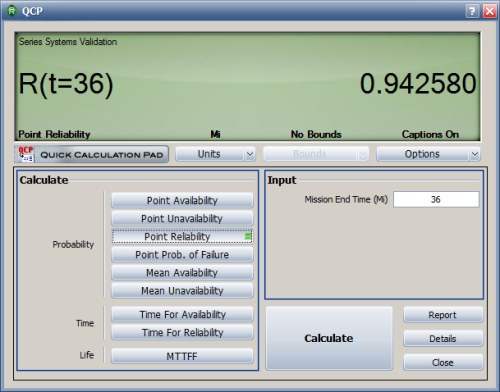
The point reliability at 36,000 miles is calculated in the QCP as 94.2580%.
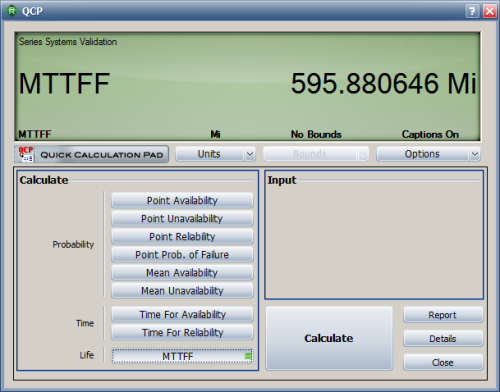
And the mean time to first failure (MTTFF), which is the mean mileage to first failure, is obtained as 595.880646 miles.
Both results are within 0.2% error. More accurate results may be obtained via simulation if the number of simulations is increased.