Inverse Power Law (IPL)-Lognormal Model

This example validates the calculations for the IPL life stress relationship with a lognormal distribution in Accelerated Life Testing (ALTA) life-stress data folios.

Reference Case

The data set is from Example 19.10 on page 504 in book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998.

Data

A Mylar-Polyurethane insulating structure was tested under several different voltage settings. The following table shows the test data.

Time Failed (Hr)	Voltage (kV)
15	219
16	219
36	219
50	219
55	219
95	219
122	219
129	219
625	219
700	219
49	157.1
99	157.1
154.5	157.1
180	157.1
291	157.1
447	157.1
510	157.1
600	157.1
1656	157.1
1721	157.1
188	122.4
297	122.4
405	122.4
744	122.4
1218	122.4
1340	122.4
1715	122.4
3382	122.4
606	100.3
1012	100.3
2520	100.3
2610	100.3
3988	100.3
4100	100.3
5025	100.3
6842	100.3

Result

The following function is used for the Ln-Mean :

where V is the voltage and its natural log transform is used in the above life stress relation.

This function can be written in the following way:

The above equation is the general log-linear model in Weibull++. In Weibull++, the coefficients are denoted by .

In fact, the above model also can be expressed using the traditional IPL (inverse power law) model:

where and .

In the book, the following results are provided:

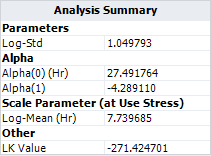
• ML estimations for the model parameters are: , and .

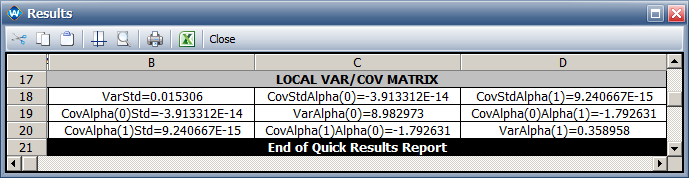
• The standard deviation of each parameter are: , and .

Therefore, their variances are: , and .

• The log-likelihood value is -271.4.

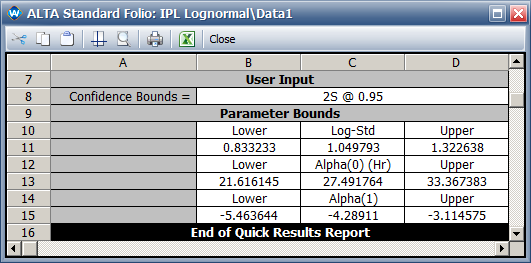
• The 95% two-sided confidence intervals are: for , it is [0.83, 1.32]; for , it is [21.6, 33.4]; and for , it is [-5.46, -3.11].

Results in Weibull++

• ML estimations for the model parameters are:

• The variance and covariance matrix for model parameters is:

• The log-likelihood value is -271.4247.

• The 95% two-sided confidence intervals are: