Median Ranks Calculation for Fractional Failures
In the September 2015 issue of Reliability HotWire, we discussed fractional failure analysis and provided an example on how to perform the analysis in Weibull++. The analysis takes into account the effectiveness of an assumed corrective action or product redesign. If the corrective action or the improvement in the redesign is not 100% effective on the failure mode being analyzed, a certain percentage of the failure mode is removed by changing it to a partial failure and a partial suspension. In this issue, we will describe how the unreliability estimates are calculated in the analysis.
The median rank method, which is used in Weibull++, estimates unreliability values based on the failure order number and the cumulative binomial distribution. When the data set contains only failures, calculation of the failure order number and the corresponding median rank value is straightforward. However, to accommodate the fractional failures in the data (partial failure and partial suspension), it is necessary to adjust the order of each failure. We will first present a method for calculating the adjusted failure order number (mean order number) for a data set that contains fractional failures, and then we will look into multiple ways to calculate the median ranks using the mean order number.
Mean Order Number (MON) Calculation
Prior to computing MON, the data points are arranged in ascending order. The MON for each failure is calculated as:
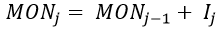
where, j is the jth failure item and Ij is the increment.
The increment, I, is defined by:

where:
N is the sample size, or total number of items in the test
PMON is the previous mean order number
NIBPSS is the number of items beyond the present suspended set
The increments are calculated for the first data point and for each suspension in the data set. For all other data points, the increment is the same as the increment for the previous data point. For example, for the data set in Table 1, the increment for the last two failures stays constant at 1.33.
| State | Time to Failure | Increment | MON |
| F | T1 | 1 | 1 |
| S | T2 | 1.333333 | - |
| F | T3 | 2.333333 | |
| F | T4 | 3.666667 |
To use the MON calculation for fractional failures, the equation should be adjusted to include the partial failure of an item. The adjusted equation can be expressed as:

where Fj is the failure fraction of the jth failure item.
Median Ranks Calculation
The rank can be found for any percentage point, P, greater than zero and less than 1, by solving the cumulative binomial equation for Z. This represents the rank, or unreliability estimate, for the jth failure in the following equation for the cumulative binomial:

where N is the sample size and j is the order number.
The median rank is the value that the true probability of failure, Q(Tj), has for the jth failure out of a sample of N units at the 50% confidence level. The median rank is obtained by solving this equation for Z at P = 0.5:

For example, if N = 4 and we have four failures, we would solve the median rank equation for the value of Z four times; once for each failure with j = 1, 2, 3 and 4, respectively. However, when there are fractional failures in the data set (or when all suspensions are not at the end of the ordered data set, as in Table 1), the j values will not necessarily be integers and we will need to use linear interpolation between the median ranks values calculated for the integers.
There are other methods for estimating median ranks. We will cover some of them briefly in the following sections.
Beta and F Distributions Approach
One of the methods for estimating median ranks is by applying two transformations to the cumulative binomial equation, first to the beta distribution and then to the F distribution. Then, the median ranks value for the jth failure is given as:

where 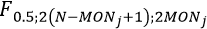 is the F distribution at the 0.50 point, with 2(N
- MONj + 1) and 2MONj degrees of freedom, for failure
j out of N units.
is the F distribution at the 0.50 point, with 2(N
- MONj + 1) and 2MONj degrees of freedom, for failure
j out of N units.
Benard's Approximation
Another quick but less accurate approximation of the median ranks is given by Benard's approximation:
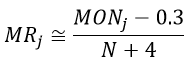
where MRj is the median ranks, MONj is the mean order number for jth failure and N is the total number of items tested.
Johnson's Approximation
Leonard Johnson defined the equations for computing the approximate median rank values as:
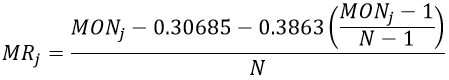
for N > 20, and:

for N ≤ 20, where MRj is the median ranks, MONj is the mean order number for jth failure and N is the total number of items tested.
Example
Suppose we have the testing failure data for a product, as shown in Table 2. We want to know the median rank for each failure. The first step is to calculate the MON for each failure in the data set.
| Number in State | Time to Failure |
| 1 | 59 |
| 0.4 | 71 |
| 1 | 95 |
| 1 | 108 |
| 1 | 137 |
| 0.7 | 154 |
| 1 | 177 |
| 1 | 199 |
| 1 | 219 |
The fractional failure at 71 hours is considered as 40% failure and 60% suspension, and the one at 154 hours is considered as 70% failure and 30% suspension. Then, the mean order numbers (MON) for each failure can be calculated via the increment method. The results are given in Table 3.
| Number in State | Time to Failures/Suspensions | Increment (I) | MONj | |
| Failures | Suspensions | |||
| 1 | 59 | 1 | 1 | |
| 0.4 | 71 | 1.4 | ||
| 0.6 | 71 | 1.075 | - | |
| 1 | 95 | 2.475 | ||
| 1 | 108 | 3.550 | ||
| 1 | 137 | 4.625 | ||
| 0.7 | 154 | 5.3775 | ||
| 0.3 | 154 | 1.15563 | - | |
| 1 | 177 | 6.533125 | ||
| 1 | 199 | 7.68875 | ||
| 1 | 219 | 8.84438 | ||
The increment and the MON for the first failure will be 1. Then the second failure, which is a fractional failure, will have a MON of 1.4 because it only had 40% failure.
When we encounter the first suspension data point, we need to calculate the increment. For example, the first increment is calculated as:

Then, the MON for the third failure can be calculated as:
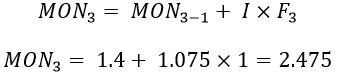
We need to pay attention to the MON calculation for the sixth failure because it is also a fractional failure and is calculated as:

After calculating the MON for each failure in the data set, we can calculate the median rank values via the interpolation method, beta and F distribution approach, Benard's approximation and Johnson's approximation. The results are given in Table 4.
| MON | Via Interpolation | Beta and F Distribution Approach | Benard's Approximation | Johnson's Approximation |
| 1 | 7.413 | 7.413 | 7.447 | 7.413 |
| 1.4 | 11.632 | 10.520 | 11.702 | 11.671 |
| 2.475 | 23.026 | 22.413 | 23.138 | 23.117 |
| 3.55 | 34.5 | 34.557 | 34.574 | 34.562 |
| 4.625 | 45.991 | 46.058 | 46.011 | 46.007 |
| 5.3775 | 54.036 | 53.967 | 54.016 | 54.019 |
| 6.533125 | 66.388 | 66.736 | 66.310 | 66.323 |
| 7.68875 | 78.720 | 79.113 | 78.604 | 78.627 |
| 8.844375 | 90.946 | 91.377 | 90.898 | 90.931 |
All the results, other than the second and third values calculated via beta and F distribution approach, are within 0.5% or less error margin. Weibull++ uses a more complex algorithm to calculate the median rank values that encompasses the beta and F distribution and interpolation approaches. The values are presented in the following figure.

Conclusion
In this article we presented the increment method for calculating the mean order number, adjusting for fractional failures. Then we provided four different approaches for calculating the median ranks based on the MON. No significant difference is observed between the methods for the given data set. However, it should be noted that the size of the difference between the methods is based on the data set being analyzed.
References
- Kececioglu, Dimitri. Reliability & Life Testing Handbook. 2 vols. Englewood Cliffs, New Jersey: Prentice Hall, Inc., 1993-94.
- "Life Data Analysis Reference Book," ReliaWiki.org, accessed September 8, 2016, https://help.reliasoft.com/reference/life_data_analysis